Crypt Key

"Crypt" means "encrypt" and "graphy" means "writing".  Cryptography is the study of writing the code in an encrypted form. 

Security in Computer Networking

Consider the today's scenario of Internet where , there are more than 2 billion Internet users throughout the Globe. People interacting with each other, exchanging mails, purchasing items online and many other activities are being done over Internet online.

Thus there is a great need of securing the data of the users from the bad commodity or person, or we can say this bad person as an Intruder.

Suppose there are 2 persons , James and Steve. They want to communicate over Internet. Lets consider a scenario, what can be there basic needs when they communicate. First of all, they both surely wanted that the data they are exchanging, must not be read by any third person, it should be between them only. Secondly, while transmitting the data, the message should not be deleted, or modified. It should reach the destination in its original form. Thirdly, they both wants to verify that the person they are communicating , is the legal person, with whom they wants to communicate. Steve wants to make sure that the person on other side is James only, and James wants to make sure, that he is communicating with Steve only.

Taking these 3 scenarios, we can say that there are some basic needs of the communicating parties. These are :

1. Confidentiality :

The term confidentiality means that the meaning of the data must be understood by the sender and the intended receiver only. As an Intruder can steal the data during its transmission. Thus the message must be encrypted, so the Intruder is unable to understand the message.

2. Integrity :

James and Steve wants to ensure that the data is not altered during its transmission  neither by an Intruder, nor accidentally. In Transport Layer and Network Layer, we have checksum for error in the message. But prior to that, Data Integrity is used for this purpose.

3. Authentication :

In real world, when you meet a person and talks to him, you both just tell your name to each other, in order to verify each other identity. But when you are communicating over Internet, and you cannot see the other party, its very difficult to authenticate the identity of that person. Thus Authentication includes verifying the identity of the person to each other over Communication Medium.

4. Organisation Security :

As you must be aware, that now a days , almost every organisation's network is connected to the outer world Internet. Thus an Intruder can get access of the Organisation Network, he can deposit harmful malwares or worms in the end systems of the organisation network, can access secret information of the organisation. To secure organisation from such attacks, we have Firewalls and Intrusion detection System in Computer Networks which we will cover in our later posts. 

Now lets have a look at what an Intruder can do and how it can harm the network. Suppose James and Steve are communicating and they want to ensure confidentiality, Data Integrity and Authentication.  Now what different things an Intruder can do.

i)   Record the messages on the channel.

ii)   Delete or Modify the original message during its transmission.

iii)   Impersonating himself as someone else.

If proper measures are not taken, then an Intruder can attack in a numerous number of ways. For example, if not properly encrypted, an Intruder can steal your username and Password. He can do Denial of Service ( DoS ) attack by overloading the network resources and disabling other Network users to communicate. There are various other attacks also. We will discuss each and there measure in detail , later in this post and in the coming post.

Till now you must have understsood that there is a great need of securing our data while transferring it over Communication medium. There are various techniques to safeguard our data, these are known as Cryptography Techniques.

Cryptographic techniques are so much much developed in past 30-40 years, that they themselves include Confidentiality, Integrity and Authentication. So there is no need of applying for different security algorithms to provide all these services individually. 

Cryptography allows a sender to be-fool an Intruder by encrypting the message in some other format using certain technique or algorithm. The Intruder can be disguised, that he cannot get any information from the data, if he is able to intercept it. Yes , the authenticated receiver will be able to receive the original data from the disguised data. 

Let us suppose , James and Steve wants to communicate. James wants to send a message to Steve.  For example: James wants to ask "How are you Steve". Thus James message in original form is known as Plain text. James will use an encryption algorithm to encrypt his original message, to save it from the intruder attack. The encrypted message is known as Cipher Text. Cipher Text is not understandable by the intruder. 

But as you know, in today's global world, almost all the encryption and decryption algorithms are open to every person on the Internet. Even intruder knows these algorithms.So if intruder knows the encryption method, he could have easily decrypt the message. But still something is there, that is preventing the intruder to decrypt and extract the transmitted message, that is known as key.

A key can be anything like a string of characters or numbers etc. Say in this case, the encryption algorithm takes key A, message m as input and produces the cipher text as output. The cipher text here will be denoted as A(m).

Cipher Text ( C ) = A(m)

This means that the plain text, m is encrypted using a key A.  On the receiving side, Steve will provide a key B and the cipher text to the decryption algorithm, that will generate the plain text.

Plain Text (m) = B (C)

or

we can also write it as   , Plain Text (m) = B(A(m))

There are two types of encryption Algorithms.

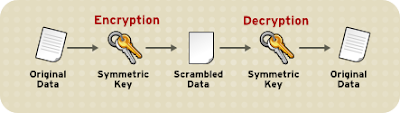
i) Symmetric Key Algorithm :

In these algorithms, both sender and receiver have the identical keys. They share it with each other secretly.

ii) Public Key Algorithm :

In these types of algorithms, sender and receiver make use of a pair of keys. One of the keys is known to both sender and receiver and infact to the rest of the world, and the other key is known only to one , either sender or receiver, but not to both.

Let us start with our discussion over different encryption Algorithm. First we will be going through Symmetric Key Algorithms and then moving on to various public key encryption techniques.

Symmetric Key Algorithm in Cryptography

Till now what have you understand about Cryptography. It must be that Cryptography is just putting one thing in place of the other using certain techniques so that it should not be understood by any wrong person. So we shall now look at various symmetric algorithms that are almost 500 years old or more. For Symmetric Key cryptography algorithms , we will use key as K. 

1. Caesar Cipher :

For example : James wants to send a message to Steve, 

       "James, Meet me at University, Steve". 

Caesar Cipher will replace the every alphabet by its K letter later in the alphabet. Say if key K=5.  Then every alphabet in the plain message will be replaced by its 5 letter later alphabet. Therefore in this case, the cipher text will be as follows.

m= James, Meet me at University, Steve

K=5

Cipher Text ( C) = K(m) = K(5) 

'J' will be replaced by 'O', 'a' will be replaced by 'f' and similarly all the letters will be replaced. So our generated cipher text would be,

Cipher Text = Ofrjx, Rjjy rj fy Zsnajwxnyd, Xyjaj

Disadvantage of Caesar Cipher

Might be , the above Cipher text looks very difficult to read or unintelligible. But as you know there are only 26 alphabets in English. Thus if the intruder came to know that Caesar Cipher is used, then its very easy for him to break the code, as there are only 25 key value possible. So he can use hit and try method for 25 times and will surely obtain the original message in one of its try. 

2. Mono-Alphabetic Cipher :

Mono-alphabetic Cipher is an improvement over Caesar cipher. In Caesar Cipher, we were only able to replace the letters according to a pattern ( substituting according to K ) . But in Mono-alphabetic Cipher, we can replace the letters randomly. This means any letter can be substituted for any letter, as long as for a single letter throughout the message, same susbstitute must be used. 

Lets take an Example of a mono-alphabetic Cipher. 

The plain message, "James, Meet me at University, Steve" will be encrypted as ,

Cipher Text = pqdtl, Dttz dt qz Xfoctklozn, Lztct

Mono-alphabetic cipher can be extended to 26! ways to encrypt your text. It is almost equal 10^26. Thus, even if the intruder knows , that you have used Mono-alphabetic cipher algorithm, then using a Brute Force Approach ( Hit and Trial Approach ) also, it will be very brainstorming task for him to crack the code.

3. Poly-alphabetic Cipher :

One more improvement of Caesar Cipher was Poly-alphabetic Cipher. In poly-alphabetic , we use 2 Caesar ciphers together. There are 2 keys such as ( with K=3 and K=5). Now we can chose that how these 2 keys should be used in a pattern. For Example: C1  , C1 , C2 , C2 , C1. The 1st letter will be encrypted using 1st encryption key, the second will also be using 1st encryption key, 3rd will be using 2nd encryption key, 4th will use 2nd key also and the 5th letter will be encrypted using 1st encryption key. And this pattern will be followed for the coming letters also. Lets take our Example :

Plain Text (m) = "James, Meet me at the University, Steve".

Keys, K=3, K=5

                           

Cipher Text (C) = Mdrjv, Phjy ph dy ykh  Xsnyhuxnwb, Vyjyh

In Poly-alphabetic Cipher, the Encryption and the Decryption key is the knowledge of the two ciphers i.e.(K=3 and K=5) and the pattern C1  , C1 , C2 , C2 , C1. 

• Since now a days , technology and the communication over Internet has grown to that extent, that these Symmetric Key Cryptographic Techniques also don't work very effectively. As the 2 commodities communicating needs to share the key. Which is not feasible. Thus these techniques are hardly in use in today's world. The techniques which are currently in use are PGP or Public Key Encryption.

Public Key Cryptography

Securing Computer Networks using Public Key

Symmetric Key Cryptographic Techniques getting obsolete with the increasing number of user over the Internet, public key cryptographic techniques came into existence and are playing a vital role in today's computer network.

In Public Key Cryptography, inspite of having a shared key between sender and receiver, there are 2 keys.
Let us Suppose, James is the sender and Steve is the receiver.
Steve will have 2 keys , one is Public Key- that is available to the whole world and the second is Private
Key- that is only known to Steve. We will use Us   for the public key of Steve and Ks   for the private key of Steve.


James in order to to send message to Steve securely, will 1st fetch the public key of Steve (that is known to everyone). Now James will encrypt message, m , using an encryption algorithm and the public key if Steve. That means, James will perform, Us (m). On receiving the encrypted message from James, Steve will use a decryption algorithm and his private key, to get the plain text. Steve will compute Ks(Us (m)). You can clearly see that, James and Steve can securely send message to each other, without sharing or distribution of any key ( that has to be done in Symmetric Key Cryptography).

But a problem arises in such cases. As the public key of Steve is well known to everyone around the globe, thus anyone can encrypt a message using using his public and send it to Steve, impersonating himself as James. In Symmetric Key cryptography, as sender and receiver share the key, they both are verified of each other identity. But this is no longer available in Public Key Cryptography, as the public key is known to everyone. Therefore, to overcome this problem of authentication, we have a phenomenon , known as Digital Signature, that I will discuss with you later.


Let us now start with some Public Key Encryption Algorithms.


RSA Encryption Algorithm


RSA was named after the scientists who developed it i.e. Ron Rivest , Adi Shamir , Leonard Adleman . Lets now see the working of of RSA. But before directly coming to the implementation of RSA, lets have a look at some mathematical calculations, as RSA makes a large use of modulo-n for computing and encrypting a data. In modulo,  if you compute A modulo n, then the result will be the remainder lest after dividing A by n. For example : If you compute 24 mod 5, the result will be 4. There are various operations associated with modulo. These are as follows.

• [( (a mod n) + ( b mod n )] mod n = (a + b) mod n

• [( (a mod n) - ( b mod n )] mod n = (a - b) mod n

• [( (a mod n) * ( b mod n )] mod n = (a * b) mod n

• ( ( a mod n)^d ) mod n = ( a^d) mod n

While you send a message to someone, it is nothing but a stream of bytes , that is following a bit pattern. And a bit pattern can be easily represented by an Integer. For Example : The bit pattern 0110 can be written as 6 , 1001 can be written as 9 and so on every bit pattern. Therefore, when you are encrypting a message using RSA, you are actually encrypting an Integer.

Now to generate a public key and a private key in RSA algorithm, Steve will perform the following steps :

1. Choose two large prime numbers  a and b.

Now a question arises, how large the numbers must be ? The answer is, as mush the numbers are large, the more harder is to break the RSA algorithm. But also, it will takes more time to compute encryption and decryption. Thus it is recommended that you use prime numbers of the order 1024 bits.

2. Calculate n = a * b and  y = ( a-1) * ( b-1 )

3. Select a number e , less than n ( e < n ) such that e and n doesn't have any common factor other than 1. Hence m and n are said to be as relatively prime.

e will be used in encrypting the message.

• 5 and 11 are relatively prime , as they have only 1 as common factor. 

4. Find a number z such that ez-1 is exactly divisible by y. We can also write it as that select z such that 

                                                         ez mod y =1.

z will be used decrypting the message.

5.  Now the public and the private key of Steve are ready. The public key , Us that will be available to the whole world is  ( n, e) and his private key , Ks is  ( n, z ).

\

James is sending a message m to Steve. Message will be represented by some integer that can be mathematically computed. Thus James will encrypt the message in this way.

Cipher text or Encrypted Message ( c ) = ( m^e ) mod n

The bit pattern corresponding to c, will be sent to Steve.

On the receiving side, to get the original message, Steve will decrypt it in the following way.

Plain text ( m ) = ( c^z ) mod n.

Let us take an Example that will make clear , how the RSA algorithm works.

Suppose James has a message , m=5 that he wants to send to Steve. So he start with RSA algorithm.

1. He chooses two prime numbers, say a = 17 and b = 7 .

2. Calculate n= a * b= 17 * 7 = 119 and y = ( 17-1 ) * ( 7-1 ) = 16 * 6 = 96.

3. Select e=5. Thus 5 and 119 are relatively prime.

4. To calculate in order to fulfill ez mod y=1. We will get z as 77. 

5. Therefore Steve public key = ( 119, 5) and private key = ( 119, 77). 

Thus while encrypting the message before sending it, James will do the following computation. 

Cipher Text ( c ) = ( m^e) mod n  = ( 5^5) mod 119 = 3125 mod 119 = 31

On the receiving side, while decrypting the cipher text, Steve will do the following computation.

Plain Text ( m ) = (c^z) mod n = ( 31^77) mod 119 = 5

So you must have noticed that , RSA is secure in the sense, there are numerous number of prime numbers are there for computation. Hence it will be a very brainstorming task for an Intruder to break the code and get the plain text.

IEEE 802 Standards List

List of the IEEE 802 Standards and Working Groups

IEEE 802.1     Higher Layer LAN Protocols Working Group dealing with Bridging (networking) and                                  Network Management

IEEE 802.2     Logical Link Control

IEEE 802.3     Ethernet Working Group

IEEE 802.4     Token Bus

IEEE 802.5    Token Ring MAC protocol definitions

IEEE 802.6    early  MANs (Dual queue dual bus)

IEEE 802.7     Broadband LAN using Coaxial Cable

IEEE 802.8     Fiber Optic TAG

IEEE 802.9     Integrated Services LAN (ISLAN or isochronous Ethernet)

IEEE 802.10   Inter-operable(vurtual) LANs and security

IEEE 802.11   Wireless LAN & Mesh (Wi-Fi certification) Group
        IEEE 802.11a 
        IEEE 802.11b
        IEEE 802.11g
        IEEE 802.11n
        IEEE 802.11ac
        IEEE 802.11ad
        IEEE 802.11af
        IEEE 802.11ai
        IEEE 802.11aj
        IEEE 802.11aq
        IEEE 802.11ax

IEEE  802.12  Demand priority (HP's AnyLAN)100BaseVG

IEEE 802.13   Fast Ethernet Development

IEEE 802.14   Cable Modems

IEEE 802.15   Wireless Personal Area Network (WPAN) Working Group

         IEEE 802.15.1     Bluetooth Certification

         IEEE 802.15.2     IEEE 802.15 and IEEE 802.11 coexistence

         IEEE 802.15.3     High-Rate Wireless PANs; eg: Ultra Wide Band(UWB),..

         IEEE 802.15.4     Low-Rate Wireless PANs; eg: Zigbee, WirelessHART, MiWi,..

         IEEE 802.15.5     Mesh networking for WPAN

         IEEE 802.15.6     Body Area Network (BAN)

IEEE 802.16   Broadband Wireless Access (Wimax certification)

         IEEE 802.16.1 Local Multipoint Distribution Service (LMDS) 

IEEE 802.17   Resilient Packet Ring

IEEE 802.18   Radio Regulatory TAG

IEEE 802.19   Wireless Coexistence Working Group     

IEEE 802.20   Mobile Broadband Wireless Access IEEE 802.21   Media Independent Handoff Services Working Group IEEE 802.22  Wireless Regional Area Network IEEE 802.23  Emergency Services Working Group IEEE 802.24  Smart Grid TAG IEEE 802.25  Omni-Range Area Network

Steps occur when you enter your credit card number online 

RSA - Rivest, Adi Shamir, and Leonard Adleman, 

This idea firstly came to the scientist named Pierre Fermat.

Prime Numbers 1 , 3, 5, ... play a major and important key role in our lives knowing or unknowingly.

I can tell something’s up when random people start asking me about the randomness of primes—without even knowing that I’m a mathematician! In the past couple of weeks we’ve heard about a beautiful result on the gaps between primes and about cicadas’ prime-numbered life cycles.

Our current love affair with primes notwithstanding, many people have wondered whether this is all just abstract theoretical stuff or whether prime numbers have real-world applications.

In fact, they have applications to something as ubiquitous and mundane as making a purchase online.

Every time you enter your credit card number on the Internet, prime numbers spring into action. Before your card number is sent over the wires, it must be encrypted for security, and once it’s received by the merchant, it must be decrypted.

One of the most common encryption schemes, the RSA algorithm, is based on prime numbers. It uses a “public key,” information that is publicly available, and a “private key,” something that only the decoding party (merchant) has. Roughly speaking, the public key consists of a large number that is the product of two primes, and the private key consists of those two primes themselves. It’s very difficult to factor a given large number into primes. For example, it took researchers two years recently to factor a 232-digit number, even with hundreds of parallel computers. That’s why the RSA algorithm is so effective.

Definition: Prime numbers are whole numbers greater than 1 that are not divisible by any whole number other than 1 and itself. The first few are 2, 3, 5, 7, 11, 13 … 

To explain how the RSA algorithm works, I need to tell you first about something called Fermat’s little theorem. It was discovered by Pierre Fermat, the same French mathematician who came up with the famous Fermat’s last theorem. 

Fermat had a penchant for being cryptic; in the case of his last theorem, he left a note on the margin of a book stating his theorem and adding: “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.” Call it the 17^th-century version of a Twitter proof. Many professional mathematicians and amateurs tried to reproduce Fermat’s purported proof, and it took more than 350 years to come up with a real one. 

About Andrew Wiles in the next post

To understand what Fermat’s little theorem means, we need to learn how to do arithmetic “modulo N.” This is something, in fact, we do all the time when adding angles. If you rotate an object by 180 degrees, and then by another 270 degrees, the net result will be rotation by 90 degrees.

 That’s because 180 + 270 = 450, and then we subtract 360 from it, because rotation by 360 degrees means no net rotation at all. This is what mathematicians call addition “modulo 360.” Likewise, we can do addition modulo any whole number N instead of 360. 

(Another familiar example is adding hours, where N = 12.) 

And we can also do multiplication modulo N.

Now suppose that N is a prime number. Then we have the following remarkable fact: Raising any number to the N^th power modulo N, we get back that same number. For example, if N = 5, then the 5^th power of 1 is 1 and the 5^th power of 2 is 32, which is equal to 2 modulo 5 because after you subtract the closest multiple of 5 (in this case, you subtract 30, or 5 × 6), you are left with 2 (because 32 = 5 × 6 + 2). Likewise, the 5^th power of 3 is equal to 3 modulo 5, and so on. This is Fermat's little theorem. Fermat first divulged it in a letter to a friend. “I would send you a proof of it,” he wrote, “but I am afraid it’s too long.” He was such a tease, this Fermat. Unlike the proof of his last theorem, however, the proof of the little one is surprisingly simple—it could even fit in the margin of a book. I would write it here, but my editor tells me that my article is already too long.

No worries though, you can read the proof in this excerpt from my book Love and Math.

This is neat, but what does it have to with Internet security?

We need to devise a two-step procedure:

First encrypt a credit card number and then decrypt it, so that if we follow both steps we get back the original number. The good news from Fermat’s little theorem is that raising a card number to a prime power modulo that prime is a procedure that gives us back the original number. The bad news is that because a prime is not divisible by anything, there is no way to break this procedure into two steps. However, Ron Rivest, Adi Shamir, and Leonard Adleman, after whom the RSA algorithm is named, were not discouraged. They took Fermat’s idea one step further. They asked: What if we take N which is the product of two primes—call them p and q. Then we have the following analogue of Fermat’s little theorem:

Raising any number to the power (p – 1)(q – 1) + 1 will give us back the same number modulo N. For example, N = 15 is the product of p = 3 and q = 5. Then (p – 1)(q – 1) + 1 = (3 – 1)(5 – 1) + 1 = 9. If you raise any number to the 9^th power, you get back the same number modulo 15. It looks like a miracle, but in fact the proof is no more complicated than that of Fermat’s little theorem.

And now we can use it for encryption: For the given prime numbers p and q, the combination (p – 1)(q – 1) + 1 will typically be a number that is not a prime. Hence it can be represented as the product of two whole numbers, call them r and s. (In our example, (p – 1)(q – 1) + 1 = 9, so we can take r = 3 and s = 3.) Raising a number to the power (p – 1)(q – 1) + 1 can now be broken into two steps: raising it to the r^th power and then raising it to the s^th power.

Here’s how it works in practice: The merchant picks two large prime numbers p and q (there are various algorithms for generating primes), takes their product N, and chooses r and s. He or she then makes r and N known to everyone; this is the public key. The encryption consists of raising a credit card number to the r^th power modulo N. Anyone can do it (on a computer, because the numbers involved are quite large).

The decryption, on the other hand, consists of raising the resulting number to the s^th power modulo N. This gives back the original credit card number (see here for more details). The merchant keeps the number s secret. Therefore the transmission of the credit card numbers is secure. The only way to find s, and hence to be able to decrypt the card numbers, is to determine the prime factors p and q of the number N. For sufficiently large N, however, using known methods of prime factorization, it may take many months to find p and q, even on a network of powerful computers. But if one could come up with a more efficient way to factor numbers into primes (for example, by using a quantum computer), then one would have a tool for breaking the RSA algorithm. That’s why a lot of research is directed toward factoring numbers into primes. Scores of legitimate mathematicians are working on this, and perhaps not so legitimate ones as well.

To an outsider, the RSA algorithm appears like a card trick: You pick a card from a stack, hide it (this is like encryption), and after some manipulations the magician produces your card—adbraka! Well, that's pretty much what the RSA algorithm does … except that the role of magic is now played by math.

RSA- Names of 3 Security Scientist Ron Rivest, Adi Shamir and Leonard Adleman 1977

 

RSA algorithm and the realization of the principle. RSA is the best tool for data encryption can be used for digital signatures, a non-symmetric cryptography algorithms. It has a pair of keys, one of which is the private key, by the user preserved another for the public key can be made public. And VC++ Language, through the MFC designed a small system to the simple application of simulation algorithm

https://www.mediafire.com/?1zs9b6vp5m09saa

News

Liz O'Donnell announced as next RSA Chairperson