Showing posts with label DS. Show all posts

Sunday 25 December 2016

KNAP

KNAPSACK PROBLEM

JUNE 2014 - PAPER III Q.No 62

62. Consider the fractional knapsack instance n=4, (p1,p2,p3,p4) = (10,10,12,18)
(w1,w2,w3,w4)=(2,4,6,9) and M=15. The maximum profit is given by,
(Assume p and w denotes profit and weights of objects respectively).
(A)40
(B)38
(C)32
(D)30
Ans:-B

Explanation:-
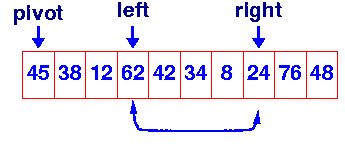
Knapsack problem can be solved either using Greedy approach or through Dynamic programming. I am going to be explaining using the former. It has been proved that for the knapsack problem using greedy method we always get the optimal solution provided the objects are arranged in decreasing order of pi/wi. So, before solving the problem, let us arrange all the objects in decreasing order of pi/wi.
Capacity of the knapsack M = 15
Number of objects = 4
Profits(p1,p2,p3,p4)=(10,10,12,18)
Weights(w1,w2,w3,w4)=(2,4,6,9)
To get the solution arrange objects in decreasing order of profit/weights as shown below.
p1/w1=10/2 =5

p2/w2=10/4=2.5

p3/w3=12/6=2

p4/w4=18/9=2

Arrange in decreasing order of pi/wi, we get

Object	Weight	Profit	Pi/wi
1	2	10	5
2	4	10	2.5
3	6	12	2
4	9	18	2

The fractions of the objects selected and the profit we get can be computed as shown below:

Remaining Capacity	Object selected	Weight of the object	Fraction of the object selected
15	1	2	1 full unit
15-2=13	2	4	1 full unit
13-4=9	3	6	1 full unit
9-6=3	4	9	3/9 or 1/3 fraction of unit

So, the solution vector will be=(1,1,1,1/3)
Profits=1 X 10 + 1 X 10 + 1 X 12 + 1/3 X 18
Profits=10+10+12+6
Profits=20+18
=38
So the correct answer will be 38. The maximum profit is given by option (B) which is 38. Solve the following problem and see.

I. Obtain the optimal solution for the knapsack problem given the following: M=40,n=3, (p1,p2,p3)=(30,40,35) and (w1,w2,w3)=(20,25,10).

. The answer for the above problem is 82.5

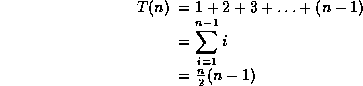
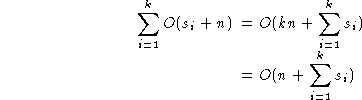
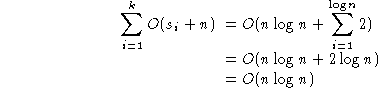INFIX EXPRESSION TO POSTFIX EXPRESSION

CONVERSION OF INFIX EXPRESSION TO POSTFIX EXPRESSION

The conventional method of representing an arithmetic expression is known as infix because the operand is placed in between the operands. If the operator is placed before the operands then this notation is called prefix or Polish notation. If the operator is placed after the operand then this notation is called postfix or reverse polish notation. So now we have three ways to represent an arithmetic expression.
Infix:   A+B

Prefix:   +AB

Postfix:   AB+

Now, let us see how to convert an infix expression to postfix expression. The rules of parenthesis and precedence would be followed in the following way. If there are parenthesis in the expression, then the portion inside the parenthesis will be converted first. After this the operations are converted according to their precedence. (* and / first, followed by + and -). If there are operators of equal precedence then the operator which is on the left is converted first. In order to understand this with an example, let us solve an example from June 2014, Paper III, Question No. 41.
JUNE 2014 - PAPER III - Q.No 41
41. The reverse polish notation equivalent to the infix expression

((A + B) * C + D) / (E + F + G)

(A) A B + C * D + E F + G + /

(B) A B + C D * + E F + G + /

(C) A B + C * D + E F G + +/

(D) A B + C * D + E + F G + /

Ans:-A
Explanation:-

First, always the expression given within parenthesis is converted first. Since there are 2 expressions with the parenthesis, I am going with the expression (E + F + G) first, although the order does not matter.

In the expression (E + F + G), there are 3 operands E,F and G and two operators, both being +. Since both the operators are the same, the expression is going to be evaluated from left to right. So E + F is considered first and converted into postfix form which is EF+. So, the expression becomes,

( ( A + B ) * C + D) / ([E F +] + G)

Any expression converted into postfix form is going to be written in square brackets.

( ( A + B ) * C + D) / [ E F + G + ]
. Here EF+ is one operand, G is another operand and + is the operator.

The next expression to be converted into postfix is ( A + B).

( [ A B + ] * C + D) / [ E F + G + ]

Now, the expression which is enclosed in parenthesis is evaluated and so, we get

( [ [ A B + ] C * ] + D) / [ E F + G + ]

[ A B + C * D + ] / [ E F + G + ]

[ A B + C * D + ] [ E F + G + ] /

So, the final postfix expression is A B + C * D + E F + G + /. This answer is available in option A. So option A is the correct answer.

PROPERTIES OF BINARY TREES

There are some basic properties of binary trees. It is better to know all of them and how to apply.For easier understanding I am giving it in a tabular form.

1.	Maximum number of nodes on any level i is	2ⁱ
2.	Maximum number of nodes possible in a binary tree of height h is	2^h-1
3.	Minimum number of nodes possible in a binary tree of height h is equal to	h
4.	If a binary tree contains n nodes, then its maximum height possible is	n
5.	If a binary tree contains n nodes, then its minimum height possible is	log₂(n+1)
6.	In a non empty binary tree, if n is the total number of nodes and e is the total number of edges, then	e=n-1
7.	In a full binary tree of height k, there are	2^k-1 internal nodes
8.	A strictly binary tree with n leaf nodes always has	2n - 1 nodes

JUNE 2007 - PAPER II Q.No 3

The maximum number of nodes in a binary tree of depth 10 is :
(A). 1024
(B). 2¹⁰-1
(C). 1000
(D). None of the above
Ans:- B
Explanation:-
According to property 2, the maximum number of nodes in a binary tree of height or depth h is 2^h-1

DECEMBER 2007 - PAPER II Q.No 23

The height of a binary tree with 'n' nodes in the worst case is

(A). 0(log n)
(B). O(n)
(C). Ω(n log n)
(D). Ω(n²)
Ans:- B
Explanation:-
Big omega notation is used for representing the best case. Big oh notation is used for representing the worst case. It is a measure of the longest amount of time it could possibly take for any algorithm to complete. Since we are representing the height of a binary tree, it would be the maximum height possible in a tree with 'n' nodes and it is O(n). So, the correct answer is B.

JUNE 2009 - PAPER II Q.No. 27

In a full binary tree of height k, there are ____________internal nodes.

(A). 2^k-1
(B). 2^k-1
(C). 2^k
(D). 2^k+1

Ans:-A
Explanation:-
Refer to the following diagram to understand the explanation. A full binary tree is one which has all the levels have maximum number of nodes in a tree.

DECEMBER 2009 - PAPER II Q.No 21

If the number of leaves in a strictly binary tree is an odd number, then what can you say with full conviction about total number of nodes in the tree?.
(A). It is an odd number.
(B). It is an even number.
(C). It cannot be equal to the number of leaves
(D). It is always greater than twice the number of leaves

Ans:-A
Explanation:-
A binary tree is a strictly binary tree if each node in the tree is either a leaf node or has exactly two children. There is no node with one child. According to its property, a strictly binary tree with n leaf nodes always has 2n-1 nodes. Let us consider n to be an odd number and give it a value of 3. So, the number of nodes in the tree would be 2n - 1 which is 2 X 3 -1 = 5. So that is also an odd number. So, the answer is A.

JUNE 2010 - PAPER II Q.No 23

In a complete binary tree of n nodes, how far are the two most distant nodes?.Assume each edge in the path count as 1.
(A). About log₂n
(B). About 2log₂n
(C). About nlog₂n
(D). About 2n

Ans:-A
Explanation:-
The height h of a complete binary tree with n nodes is at the most O(log₂n).

DECEMBER 2011 - PAPER II Q.No. 50

The number of nodes in a complete binary tree of height h (with roots at level 0) is equal to

(A) 2⁰+2¹+......+2^h
(B) 2⁰+2¹+......+2^h-1
(C) 2⁰+2¹+......+2^h+1
(D) 2¹+......+2^h+1

Ans:-A
Explanation:-
Count the number of nodes in each level, starting with the root, assuming that each level has the maximum number of nodes.
n=1+2+4+....2^h-1+2^h

Data Structures

This particular question is not clear for few readers. So, I am taking it up once again.
25. Which of the following can be the sequence of nodes examined in binary search tree while searching for key 88 ?

(A) 90, 40, 65, 50, 88
(B) 90, 110, 80, 85, 88
(C) 190, 60, 90, 85, 88
(D) 65, 140, 80, 70, 88

Ans:- B
Explanation:-
I am taking the liberty of retaining an explanation given for a similar question from yahoo answers.

Best Answer: For a binary search tree, the entire tree is sorted such that for any node, every node to the left is less than the current node value and every node to the right is more than the current node value.
When walking a BST tree, you "zero in" on the value by following the correct nodes down the tree. Ideally you work closer and closer to your answer, kind of like the "guess the number" game where you give "nope, more!" and "nope, less!" hints.
a) 2, 399, 387, 219, 266, 382, 381, 278, 363
This sequence is possible.
b) 935, 278, 347, 621, 299, 392, 358, 363
This sequence is not possible. Since 621 is to the right of 347, every other node under 621 must ALSO be to the right of 347. 299 is not -- so this is an impossible walk. Basically, once you pass 347, 299 is swinging too far in the opposite direction.
c) 924, 220, 911, 244, 898, 258, 362, 363
This sequence is possible.
d) 925, 202, 911, 240, 912, 245, 363
Not possible -- 240 is to the left of 911, so every other node must also be less than 911 (but still may be to the right of 240). 912 is not to the left of 911.
e) 2, 252, 401, 398, 330, 344, 397, 363 This sequence is possible. Just barely though -- 397 is to the left of 398 but just barely!
I am taking the example b which explains why a particular sequence is not possible. Since 621 is to the right of 347, every other node under 621 must ALSO be to the right of 347.
Let us apply the same rule to all the sequences given above for us in the question.
The first sequence is 90,40,65,50,88. Do not consider any particular element as the root. But start analysing the numbers from first. 90 is the first number. 40 is the second one. So, 40 will be to the left of 90, since it is less than 90. Since 40 is to the left of 90, all numbers following 40 also should be to the left of 90, which is true in this sequence. 65,50, and 88 will be to the left of 90. So this sequence is possible.
Let us consider the second sequence which is 90,110,80,85,88. Again 90 is the first number. 110 will be to its right since it is greater than 90. So all the numbers following 110 also should be to the right of 90,but 80,85 and 88 fall to its left. So, this sequence is not possible.
Let us consider the third sequence which is 190,60,90,85,88. So, 190 is the first number. 60 is to its left. So all the other numbers following 60 should be to the left of 190, which is holding good here. 90,85 and 88 will be to the left of 190. So, this sequence is possible.
Let us consider the fourth sequence which is 65,140,80,70,88. 65 is the first number. 140 will be to its right. All the numbers following 140 should be to the right of 65 which is true. 80,70 and 88 will be to the right of 65 as well.
So, the correct answer is option B and not C.
Thank you all, for bringing this question for discussion as we have zeroed in on the right answer.

Tuesday 6 October 2015

Sorting

7 Sorting
Sorting is one of the most important operations performed by computers. In the days of magnetic tape storage before modern data-bases, it was almost certainly the most common operation performed by computers as most "database" updating was done by sorting transactions and merging them with a master file. It's still important for presentation of data extracted from databases: most people prefer to get reports sorted into some relevant order before wading through pages of data!

7.1 Bubble, Selection, Insertion Sorts

There are a large number of variations of one basic strategy for sorting. It's the same strategy that you use for sorting your bridge hand. You pick up a card, start at the beginning of your hand and find the place to insert the new card, insert it and move all the others up one place.

/* Insertion sort for integers */

void insertion( int a[], int n ) {
/* Pre-condition: a contains n items to be sorted */
    int i, j, v;
    /* Initially, the first item is considered 'sorted' */
    /* i divides a into a sorted region, x<i, and an
       unsorted one, x >= i */
    for(i=1;i<n;i++) {
        /* Select the item at the beginning of the
           as yet unsorted section */
        v = a[i];
        /* Work backwards through the array, finding where v 
           should go */
        j = i;
        /* If this element is greater than v,
              move it up one */
        while ( a[j-1] > v ) {
          a[j] = a[j-1]; j = j-1;
          if ( j <= 0 ) break;
          }
        /* Stopped when a[j-1] <= v, so put v at position j */
        a[j] = v;
        }
    }

Bubble Sort

Another variant of this procedure, called bubble sort, is commonly taught:

/* Bubble sort for integers */
#define SWAP(a,b)   { int t; t=a; a=b; b=t; }

void bubble( int a[], int n )
/* Pre-condition: a contains n items to be sorted */
    {
    int i, j;
    /* Make n passes through the array */
    for(i=0;i<n;i++)
        {
        /* From the first element to the end
           of the unsorted section */
        for(j=1;j<(n-i);j++)
           {
           /* If adjacent items are out of order, swap them */
           if( a[j-1]>a[j] ) SWAP(a[j-1],a[j]);
           }
        }
    }

Analysis

Each of these algorithms requires n-1 passes: each pass places one item in its correct place. (The n^th is then in the correct place also.) The i^th pass makes either ior n - i comparisons and moves. So:

or O(n²) - but we already know we can use heaps to get an O(n logn) algorithm. Thus these algorithms are only suitable for small problems where their simple code makes them faster than the more complex code of the O(n logn) algorithm. As a rule of thumb, expect to find an O(n logn) algorithm faster for n>10 - but the exact value depends very much on individual machines!. They can be used to squeeze a little bit more performance out of fast sort algorithms -

Key terms

Bubble, Insertion, Selection Sorts: Simple sorting algorithms with O(n²) complexity - suitable for sorting small numbers of items only.

Binary Sort

7.4 Bin Sort
Assume that in the bin sort

the keys of the items that we wish to sort lie in a small fixed range and
that there is only one item with each value of the key.

Then we can sort with the following procedure:

Set up an array of "bins" - one for each value of the key - in order,
Examine each item and use the value of the key to place it in the appropriate bin.

Now our collection is sorted and it only took n operations, so this is an O(n) operation. However, note that it will only work under very restricted conditions.

Constraints on bin sort

To understand these restrictions, let's be a little more precise about the specification of the problem and assume that there are m values of the key. To recover our sorted collection, we need to examine each bin. This adds a third step to the algorithm above,

Examine each bin to see whether there's an item in it.

which requires m operations. So the algorithm's time becomes: T(n) = c₁n + c₂m and it is strictly O(n + m). Now if m <= n, this is clearly O(n). However if m >> n, then it is O(m). For example, if we wish to sort 10⁴ 32-bit integers, then m = 2³² and we need 2³² operations (and a rather large memory!).
For n = 10⁴:

nlogn ~ 10⁴ x 13 ~ 2¹³ x 2⁴ ~ 2¹⁷ So quicksort or heapsort would clearly be preferred. An implementation of bin sort might look like:

#define EMPTY -1 /* Some convenient flag */
void bin_sort( int *a, int *bin, int n ) {
    int i;
    /* Pre-condition: for 0<=i<n : 0 <= a[i] < M */
    /* Mark all the bins empty */
    for(i=0;i<M;i++) bin[i] = EMPTY;
    for(i=0;i<n;i++)
        bin[ a[i] ] = a[i];
    }

main() {
    int a[N], bin[M];    /* for all i: 0 <= a[i] < M */
    .... /* Place data in a */
    bin_sort( a, bin, N );

If there are duplicates, then each bin can be replaced by a linked list. The third step then becomes:

Link all the lists into one list.

We can add an item to a linked list in O(1) time. There are n items requiring O(n) time. Linking a list to another list simply involves making the tail of one list point to the other, so it is O(1). Linking m such lists obviously takes O(m) time, so the algorithm is still O(n+m). In contrast to the other sorts, which sort in place and don't require additional memory, bin sort requires additional memory for the bins and is a good example of trading space for performance.

Although memory tends to be cheap in modern processors -
so that we would normally use memory rather profligately to obtain performance,
memory consumes power
and in some circumstances, eg computers in space craft,
power might be a higher constraint than performance.

Having highlighted this constraint, there is a version of bin sort which can sort in place:

#define EMPTY -1 /* Some convenient flag */
void bin_sort( int *a, int n ) {
    int i;
    /* Pre-condition: for 0<=i<n : 0 <= a[i] < n */
    for(i=0;i<n;i++)
 if ( a[i] != i )
            SWAP( a[i], a[a[i]] );
    }

However, this assumes that there are n distinct keys in the range 0 .. n-1. In addition to this restriction, the SWAP operation is relatively expensive, so that this version trades space for time. The bin sorting strategy may appear rather limited, but it can be generalised into a strategy known as Radix sorting.

Radix

7 Radix Sorting
The bin sorting approach can be generalised in a technique that is known as radix sorting.

An example

Assume that we have n integers in the range (0,n²) to be sorted. (For a bin sort, m = n², and we would have an O(n+m) = O(n²) algorithm.) Sort them in two phases:

Using n bins, place a_i into bin a_i mod n,
Repeat the process using n bins, placing a_i into bin floor(a_i/n), being careful to append to the end of each bin.

This results in a sorted list. As an example, consider the list of integers:

36 9 0 25 1 49 64 16 81 4

Bin	0	1	2	3	4	5	6	7	8	9
Content	`0`	`1 81`	-	-	`64 4`	`25`	`36 16`	-	-	`9 49`

n is 10 and the numbers all lie in (0,99). After the first phase, we will have: Bin 0 1 2 3 4 5 6 7 8 9 Content 0 1 81 - - 64 4 25 36 16 - - 9 49 Note that in this phase, we placed each item in a bin indexed by the least significant decimal digit.
Repeating the process, will produce:

Bin	0	1	2	3	4	5	6	7	8	9
Content	`0 1 4 9`	`16`	`25`	`36`	`49`	`-`	`64`	`-`	`81`	`-`

In this second phase, we used the leading decimal digit to allocate items to bins, being careful to add each item to the end of the bin.
We can apply this process to numbers of any size expressed to any suitable base or radix.

7.5.1 Generalised Radix Sorting

We can further observe that it's not necessary to use the same radix in each phase, suppose that the sorting key is a sequence of fields, each with bounded ranges, eg the key is a date using the structure:

typedef struct t_date {
    int day;
    int month;
    int year; 
} date;

If the ranges for day and month are limited in the obvious way, and the range for year is suitably constrained, eg 1900 < year <= 2000, then we can apply the same procedure except that we'll employ a different number of bins in each phase. In all cases, we'll sort first using the least significant "digit" (where "digit" here means a field with a limited range), then using the next significant "digit", placing each item after all the items already in the bin, and so on. Assume that the key of the item to be sorted has k fields, f_i|i=0..k-1, and that each f_i has s_i discrete values, then a generalised radix sort procedure can be written:

radixsort( A, n ) { for(i=0;i<k;i++) { for(j=0;j<s_i;j++) bin[j] = EMPTY;	O(s_i)
for(j=0;j<n;j++) { move A_i to the end of bin[A_i->f_i] }	O(n)
for(j=0;j<s_i;j++) concatenate bin[j] onto the end of A; } }	O(s_i)

Total

Now if, for example, the keys are integers in (0,b^k-1), for some constant k, then the keys can be viewed as k-digit base-b integers.
Thus, s_i = b for all i and the time complexity becomes O(n+kb) or O(n). This result depends on k being constant.
If k is allowed to increase with n, then we have a different picture. For example, it takes log₂n binary digits to represent an integer <n. If the key length were allowed to increase with n, so that k = logn, then we would have:

.
Another way of looking at this is to note that if the range of the key is restricted to (0,b^k-1), then we will be able to use the radixsort approach effectively if we allow duplicate keys when n>b^k. However, if we need to have unique keys, then k must increase to at least log_bn. Thus, as n increases, we need to have logn phases, each taking O(n) time, and the radix sort is the same as quick sort!

Sample code

This sample code sorts arrays of integers on various radices: the number of bits used for each radix can be set with the call to SetRadices. The Bins class is used in each phase to collect the items as they are sorted. ConsBins is called to set up a set of bins: each bin must be large enough to accommodate the whole array, so RadixSort can be very expensive in its memory usage!

Quickk Sort

Quick Sort

Features

Similar to mergesort - divide-and-conquer recursive algorithm
One of the fastest sorting algorithms
Average running time O(NlogN)
Worst-case running time O(N²)

Basic idea

Pick one element in the array, which will be the pivot.
Make one pass through the array, called a partition step, re-arranging the entries so that:

the pivot is in its proper place.
entries smaller than the pivot are to the left of the pivot.
entries larger than the pivot are to its right.

Recursively apply quicksort to the part of the array that is to the left of the pivot,
and to the right part of the array.

Algorithm

STEP 1. Choosing the pivot
Choosing the pivot is an essential step.
Depending on the pivot the algorithm may run very fast, or in quadric time.:

Some fixed element: e.g. the first, the last, the one in the middle

Randomly chosen (by random generator ) - still a bad choice.
The median of the array (if the array has N numbers, the median is the [N/2] largest number. This is difficult to compute - increases the complexity.
The median-of-three choice: take the first, the last and the middle element.
Choose the median of these three elements.

Example:
8, 3, 25, 6, 10, 17, 1, 2, 18, 5
The first element is 8, the middle - 10, the last - 5.
The three elements are sorted: [5, 8, 10] and the middle element is 8. This is the median.
STEP 2. Partitioning
Partitioning is illustrated on the above example.
After finding the pivot the array will look like this:
5, 3, 25, 6, 8, 17, 1, 2, 18, 10 1. The first action is to get the pivot out of the way - swap it with the next to the last element
5, 3, 25, 6, 18, 17, 1, 2, 8, 10
2. We want larger elements to go to the right and smaller elements to go to the left.
Two "fingers" are used to scan the elements from left to right and from right to left:


[5, 3, 25, 6, 18, 17, 1, 2, 8, 10]
   ^                     ^
   i                     j

Note: we know that the first element is smaller than the pivot, so the first element to be processed is the element to the right. The last two elements are the pivot and an element greater than the pivot, so they are not processed.

While i is to the left of j, we move i right, skipping all the elements
less than the pivot. If an element is found greater then the pivot, i stops
While j is to the right of i, we move j left, skipping all the elements
greater than the pivot. If an element is found less then the pivot, j stops
When both i and j have stopped, the elements are swapped.
When i and j have crossed, no swap is performed, scanning stops,
and the element pointed to by i is swapped with the pivot .

In the example the first swapping will be between 25 and 2, the second between 18 and 1.
3. Restore the pivot.
After restoring the pivot we obtain the following partitioning into three groups:
[5, 3, 2, 6, 1] [ 8 ] [18, 25, 17, 10]
STEP 3. Recursively quicksort the left and the right parts

Code


if( left + 10 <= right)
    {
 int i = left, j = right - 1;
 for ( ; ; )
   {
     while (a[++i] < pivot  ) {}   // move the left finger
     while (pivot  < a[--j] ) {}   // move the right finger

     if (i < j) swap (a[i],a[j]);  // swap 
            else  break;    // break if fingers have crossed
          }
       swap (a[I], a[right-1]);    // restore the pivot
       quicksort ( a, left, i-1);   // call quicksort for the left part
       quicksort (a, i+1, right);   // call quicksort for the left part
     }
else  insertionsort (a, left, right);

here

Animation:

http://math.hws.edu/TMCM/java/xSortLab/

Implementation notes


A.
 while (a[++i] < pivot) {}
 while (pivot < a[--j]) {}

 if (i < j) swap (a[i], a[j]);
 else break;

B.

 while (a[i] < pivot) {i++;}
 while (pivot < a[j] ) {j--;}

 if (i < j) swap (a[i], a[j]);
 else break;

Complexity of Quicksort

Worst-case: O(N²)

This happens when the pivot is the smallest (or the largest) element.
Then one of the partitions is empty, and we repeat recursively the procedure for N-1 elements.

Best-case O(NlogN)

There are logN partitions, and to obtain each partitions we do N comparisons
(and not more than N/2 swaps). Hence the complexity is O(NlogN)

Average-case

O(NlogN)

Analysis

T(N) = T(i) + T(N - i -1) + cN

the time to sort the left partition with i elements, plus
the time to sort the right partition with N-i-1 elements, plus
the time to build the partitions

6. 1. Worst case analysis

T(N) = T(N-1) + cN, N > 1

T(N-1) = T(N-2) + c(N-1)
T(N-2) = T(N-3) + c(N-2)
T(N-3) = T(N-4) + c(N-3)
T(2) = T(1) + c.2

T(N) + T(N-1) + T(N-2) + … + T(2) =
= T(N-1) + T(N-2) + … + T(2) + T(1) + c(N) + c(N-1) + c(N-2) + … + c.2
T(N) = T(1) + c(2 + 3 + … + N)
T(N) = 1 + c(N(N+1)/2 -1)

Therefore T(N) = O(N²)

6. 2. Best-case analysis:

T(N) = 2T(N/2) + cN

T(N) / N = T(N/2) / (N/2) + c

T(N/2) / (N/2) = T(N/4) / (N/4) + c
T(N/4) / (N/4) = T(N/8) / (N/8) + c
……
T(2) / 2 = T(1) / (1) + c

T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + …. + T(2) / 2 =
= (N/2) / (N/2) + T(N/4) / (N/4) + … + T(1) / (1) + c.logN

T(N)/N = T(1) + cLogN = 1 + cLogN
T(N) = N + NcLogN
Therefore T(N) = O(NlogN)

6. 3. Average case analysis

T(N) = O(NlogN)

T(i)

1/N

T(0)

T(N-1)

1/N S T(j), j = 0 thru N-1
T(N) = 2/N (S T(j)) + cN

NT(N) = 2(S T(j)) + cN*N

(N-1)T(N-1) = 2(S T(j)) + c(N-1)², j = 0 thru N-2

NT(N) - (N-1)T(N-1) = 2T(N-1) + 2cN -c

NT(N) = (N+1)T(N-1) + 2cN

T(N)/(N+1) = T(N-1)/N + 2c/(N+1)

T(N)/(N+1) = T(N-1)/N + 2c/(N+1)
T(N-1)/(N) = T(N-2)/(N-1)+ 2c/(N)
T(N-2)/(N-1) = T(N-3)/(N-2) + 2c/(N-1)
….
T(2)/3 = T(1)/2 + 2c /3

T(N)/(N+1) = T(1)/2 +2c S (1/j), j = 3 to N+1
T(N) = (N+1)(1/2 + 2c S(1/j))

T(N) = O(NlogN)

Conclusions

Advantages

One of the fastest algorithms on average.
Does not need additional memory (the sorting takes place in the array - this is called in-place processing). Compare with mergesort: mergesort needs additional memory for merging.

Disadvantages:

Applications:

Never

guaranteed response time

Life-critical (medical monitoring, life support in aircraft and space craft)
Mission-critical (monitoring and control in industrial and research plants
handling dangerous materials, control for aircraft, defense, etc)

unless you assume the worst-case response time

Comparison with heapsort

both algorithms have O(NlogN) complexity
quicksort runs faster, (does not support a heap tree)
the speed of quick sort is not guaranteed

Comparison with mergesort:

mergesort guarantees O(NlogN) time, however it requires additional memory with size N.
quicksort does not require additional memory, however the speed is not quaranteed
usually mergesort is not used for main memory sorting, only for external memory sorting.

O(nlog n)

In general,

no.

Learning Goals

Be able to explain how quicksort works and what its complexity is (worst-case, best-case, average case).
Be able to compare quicksort with heapsort and mergesort.
Be able to explain the advantages and disadvantages of quicksort,
and its applications.

Exam-like questions

Briefly describe the basic idea of quicksort.

What is the complexity of quicksort?

Analyze the worst-case complexity solving the recurrence relation.

Analyze the best-case complexity solving the recurrence relation.

Compare quicksort with mergesort and heapsort.

What are the advantages and disadvantages of quicksort?

Which applications are not suitable for quicksort and why?

Quick S

Sorting Algorithms - QUICKSORT

Example


if( left + 10 <= right)
    {
 int i = left, j = right - 1;
 for ( ; ; )
   {
     while (a[++i] < pivot  ) {}   // move the left finger
     while (pivot  < a[--j] ) {}   // move the right finger

     if (i < j) swap (a[i],a[j]);  // swap 
            else  break;    // break if fingers have crossed
          }
       swap (a[i], a[right-1]);    // restore the pivot
       quicksort ( a, left, i-1);   // call quicksort for the left part
       quicksort (a, i+1, right);   // call quicksort for the left part
     }
else  insertionsort (a, left, right);

Let's see how this code will work on an example, disregarding the first if statement - the check for the number of elements.
Source array to be sorted: 10, 3, 25, 6, 8, 17, 1, 2, 18, 5 I. Compute the first partitioning:
Source array: 10, 3, 25, 6, 8, 17, 1, 2, 18, 5

Choosing the pivot:

The median-of-three: [10, 8, 5] : the median is 8

Order the three elements and hide the pivot :

5, 3, 25, 6, 8, 17, 1, 2, 18, 10
5, 3, 25, 6, 18, 17, 1, 2, 8, 10

Start rearranging:

Set two indices: i and j
i = left (i.e. i = 0)
j = right -1 (i.e. j = 8)



5, 3, 25, 6, 18, 17, 1, 2, 8, 10
^                          ^
i                          j

At each run of the for loop we swap two elements
3.1. First run: while (a[++i] < pivot ){}
++i means: first increment i, then perform the comparison.
Move i to the right skipping elements that are less than the pivot
We know that the very first element is less than the pivot, so we do not compare it



5, 3, 25, 6, 18, 17, 1, 2, 8, 10
      ^                    ^
      i                    j

i stops at 25, as 25 is greater than the pivot ( i = 2)
while (pivot < a[--j] ) {}
Initially j is 'right'-1 = 8. This is the pivot.
We do not process the pivot, that is why we write --j - first decrement, and then compare.


5, 3, 25, 6, 18, 17, 1, 2, 8, 10
      ^                 ^
      i                 j

j stops at 2 , the first element from right to left that is smaller than 8. (j = 7)
if (i < j) swap (a[i], a[j]);
else break;
i = 2 is less than j=7 and we swap 25 and 2:


5, 3, 2, 6, 18, 17, 1, 25, 8, 10
      ^                 ^
      i                 j

3.2. Second run of the for loop:


5, 3, 2, 6, 18, 17, 1, 25, 8, 10
      ^                 ^
      i                 j

We start with i = 2 , pointing to 2, and j = 7, pointing to 25
while (a[++i] < pivot) {}
6 is less then the pivot (8), we skip it, and i stops at 18 ( i = 4)


5, 3, 2, 6, 18, 17, 1, 25, 8, 10
             ^         ^
             i         j

while (pivot < a[--j]) {}
1 is less than the pivot, j stops there. (j = 6)


5, 3, 2, 6, 18, 17, 1, 25, 8, 10
             ^      ^
             i      j

if (i < j) swap (a[i], a[j]);
else break;
i = 4 is less than j = 6 and we swap 18 and 1:


5, 3, 2, 6, 1, 17, 18, 25, 8, 10
            ^       ^
            i       j

3.3. Third run of the for loop:
We start with i = 4 , pointing to 1, and j = 6, pointing to 18.


5, 3, 2, 6, 1, 17, 18, 25, 8, 10
            ^       ^
            i       j

while (a[++i] < pivot {}
17 is greater than the pivot and i stops there (i = 5)
while (pivot < a[--j] < {}
1 is less then the pivot and j stops there ( j = 4)


5, 3, 2, 6, 1, 17, 18, 25, 8, 10
            ^   ^
            j   i

if (i < j) swap (a[i], a[j]);
else break;
Now we break, because i and j have crossed

Bring back the pivot:

5, 3, 2, 6, 1, 8, 18, 25, 17, 10

[ 5, 3, 2, 6, 1 ] [8] [18, 25, 17, 10]

II. Recursively we process the left part of the array: 5, 3, 2, 6, 1

Choosing the pivot: the median of three: 5, 2, 1:

The median is 2

Order the three elements and hide the pivot:

1, 3, 6, 2, 5

Start the for loop.

i will stop at 3 ( i = 1) - the first element greater than the pivot:
j will stop at 1 (j = 0)- the first element from right to left smaller than the pivot.

Bring back the pivot: swap the pivot with a[1]

[ 1 ] [ 2 ] [ 6, 3, 5 ]

III. Do the same with the left array and the right array.
The left array consists only of one element, so we stop.
In practice, we stop partitioning when the elements are small in number, e.g. n < 10,
and we sort with insertion sort. Here we stop at 1, for the sake of the example.
Next comes the right array: [ 6, 3, 5]
It is only of three elements, and the median of three choice will put them in order:
3, 5, 6
Now we have a sorted part: 1, 2, 3, 5, 6
IV. In a similar way we process the right part in the first partitioning: 18, 25, 17, 10.
After it has been sorted, we will obtain:
[1, 2, 3, 5, 6] [8] [10, 17, 18, 25] and this is the whole array sorted.

Quick SOrt

Quick Sort: Partition in place
Most implementations of quick sort make use of the fact that you can partition in place by keeping two pointers: one moving in from the left and a second moving in from the right. They are moved towards the centre until the left pointer finds an element greater than the pivot and the right one finds an element less than the pivot. These two elements are then swapped. The pointers are then moved inward again until they "cross over". The pivot is then swapped into the slot to which the right pointer points and the partition is complete.

int partition( void *a, int low, int high )
  {
  int left, right;
  void *pivot_item;
  pivot_item = a[low];
  pivot = left = low;
  right = high;
  while ( left < right ) {
    /* Move left while item < pivot */
    while( a[left] <= pivot_item ) left++;
    /* Move right while item > pivot */
    while( a[right] > pivot_item ) right--;
    if ( left < right ) SWAP(a,left,right);
    }
  /* right is final position for the pivot */
  a[low] = a[right];
  a[right] = pivot_item;
  return right;
  }

Note that this above code does not check that left does not exceed the array bound. You need to add this check, before performing the swaps - both the one in the loop and the final one outside the loop. partition ensures that all items less than the pivot precede it and returns the position of the pivot. This meets our condition for dividing the problem: all the items in the lower half are known to be less than the pivot and all items in the upper half are known to be greater than it.
Note that we have used our ItemCmp function in the partition function. This assumes that there is an external declaration for ItemCmp and that in any one program, we only want to sort one type of object. Generally this will not be acceptable, so the formal specification for quicksort in the Unix and ANSI C libraries includes a function compar which is supplied to qsort when it is called. Passing the function, compar, which defines the ordering of objects when qsort is called avoids this problem in the same way that we passed an ItemCmp function to ConsCollection

Analysis

The partition routine examines every item in the array at most once, so it is clearly O(n). Usually, the partition routine will divide the problem into two roughly equal sized partitions. We know that we can divide n items in half log₂n times. This makes quicksort a O(nlogn) algorithm - equivalent to heapsort.
However, we have made an unjustified assumption - see if you can identify it before you continue.http://imraan-prrec.blogspot.in/2015/10/quick.html

Quick

7.3 Quick Sort (cont)

Quick Sort - The Facts!

Quick Sort is generally the best known sorting algorithm, but it has a serious limitation, which must be understood before using it in certain applications. What happens if we apply the qsort routine on the previous page to an already sorted array? This is certainly a case where we'd expect the performance to be quite good!
However, the first attempt to partition the problem into two problems will return an empty lower partition - the first element is the smallest. Thus the first partition call simply chops off one element and calls qsort for a partition with n-1 items! This happens a further n-2 times! Each partition call still requires O(n) operations - and we have generated O(n) such calls.

In the worst case, quicksort is an O(n²) algorithm!

Can we do anything about this?

A number of variations to the simple quicksort will generally produce better results: rather than choose the first item as the pivot, some other strategies work better.

Median-of-3 Pivot

For example, the median-of-3 pivot approach selects three candidate pivots and uses the median one. If the three pivots are chosen from the first, middle and last positions, then it is easy to see that for the already sorted array, this will produce an optimum result: each partition will be exactly half (±one element) of the problem and we will need exactly ceiling(logn) recursive calls.

Random pivot

Some qsort's will simply use a randomly chosen pivot. This also works fine for sorted arrays - on average the pivot will produce two equal sized partitions and there will be O(logn) of them.

However, whatever strategy we use for choosing the pivot,
it is possible to propose a pathological case
in which the problem is not divided equally at any partition stage. Thus quicksort must always be treated as potentially O(n²).

Why bother with quicksort then?

Heap sort is always O(nlog n): why not just use it?

Heap

Algorithms for Sorting - Heapsort

Heapsort

Based on Priority Queues
Sorts in O(NlogN) time by performing N times deleteMin operations.
Why O(NlogN)?

Each deleteMin operation takes logN running time.
N times performing deleteMin → NlogN running time

Basic algorithm (not very efficient - extra memory required):

Store N elements in a binary heap tree.
Perform deleteMin operation N times, storing each element deleted from
the heap into another array.
Copy back the array.

Improvements: Use the same array to store the deleted elements
instead of using another array
How can we do this?
After each deletion we percolate down the hole that is formed after the deletion,
and as a result we get a vacant position in the array - the last cell.
There we store the deleted element.
When all the elements are deleted and stored in the same array following the above method,
the elements will be there in reversed order.
What is the remedy for this?

Store the elements in the binary heap tree in reverse order of priority -
then at the end the elements in the array will be in correct order. Complexity of heap sort: O(NlogN) is the rough estimate.
Here is an example of heapsort.

Learning Goals

Be able to explain how heapsort works and its complexity.

Exam-like questions

Explain the complexity of heapsort
Given an array e.g. 17, 23, 10, 1, 7, 16, 9, 20, sort it on paper using heapsort
Write down explicitly each step.

Heap

An Example of Heapsort:
Given an array of 6 elements: 15, 19, 10, 7, 17, 16, sort it in ascending order using heap sort.
Steps:

Consider the values of the elements as priorities and build the heap tree.

Start deleteMin operations, storing each deleted element at the end of the heap array.

After performing step 2, the order of the elements will be opposite to the order in the heap tree.
Hence, if we want the elements to be sorted in ascending order, we need to build the heap tree
in descending order - the greatest element will have the highest priority.
Note that we use only one array , treating its parts differently:

when building the heap tree, part of the array will be considered as the heap,
and the rest part - the original array.

when sorting, part of the array will be the heap, and the rest part - the sorted array.

This will be indicated by colors: white for the original array, blue for the heap and red for the sorted array
Here is the array: 15, 19, 10, 7, 17, 6

Building the heap tree

Sorting - performing deleteMax operations:

1. Delete the top element 19.

As 10 will be adjusted in the heap, its cell will no longer be a part of the heap.
Instead it becomes a cell from the sorted array

2. DeleteMax the top element 17

As 10 will be adjusted in the heap, its cell will no longer be a part of the heap.
Instead it becomes a cell from the sorted array

3. DeleteMax 16

As 7 will be adjusted in the heap, its cell will no longer be a part of the heap.
Instead it becomes a cell from the sorted array

4. DeleteMax the top element 15

As 10 will be adjusted in the heap, its cell will no longer be a part of the heap.
Instead it becomes a position from the sorted array

5. DeleteMax the top element 10.

As 7 will be adjusted in the heap, its cell will no longer be a part of the heap. Instead it becomes a cell from the sorted array

Thursday 12 February 2015

Depth-first

Pre-order

preorder(node)
  if node == null then return
  visit(node)
  preorder(node.left) 
  preorder(node.right)

iterativePreorder(node)
  parentStack = empty stack
  while (not parentStack.isEmpty() or node ≠ null)
    if (node ≠ null) 
      visit(node)
      if (node.right ≠ null) parentStack.push(node.right) 
      node = node.left   
    else     
      node = parentStack.pop()

In-order

inorder(node)
  if node == null then return
  inorder(node.left)
  visit(node)
  inorder(node.right)

iterativeInorder(node)
  parentStack = empty stack
  while (not parentStack.isEmpty() or node ≠ null)
    if (node ≠ null)
      parentStack.push(node)
      node = node.left
    else
      node = parentStack.pop()
      visit(node)
      node = node.right

Post-order

postorder(node)
  if node == null then return
  postorder(node.left)
  postorder(node.right)
  visit(node)

iterativePostorder(node)
  parentStack = empty stack  
  lastnodevisited = null 
  while (not parentStack.isEmpty() or node ≠ null)
    if (node ≠ null)
      parentStack.push(node)
      node = node.left
    else
      peeknode = parentStack.peek()
      if (peeknode.right ≠ null and lastnodevisited ≠ peeknode.right) 
        /* if right child exists AND traversing node from left child, move right */
        node = peeknode.right
      else
        visit(peeknode)
        lastnodevisited = parentStack.pop()

The term "backtrack" was coined by American mathematician D. H. Lehmer in the 1950s. Backtracking is a general algorithm for finding all (or some) solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons each partial candidate c ("backtracks") as soon as it determines that c cannot possibly be completed to a valid solution.
The classic textbook example of the use of backtracking is the eight queens puzzle, that asks for all arrangements of eight chess queens on a standard chessboard so that no queen attacks any other. In the common backtracking approach, the partial candidates are arrangements of k queens in the first k rows of the board, all in different rows and columns. Any partial solution that contains two mutually attacking queens can be abandoned, since it cannot possibly be completed to a valid solution.
Backtracking can be applied only for problems which admit the concept of a "partial candidate solution" and a relatively quick test of whether it can possibly be completed to a valid solution. It is useless, for example, for locating a given value in an unordered table
Backtracking is an important tool for solving constraint satisfaction problems, such as crosswords, verbal arithmetic, Sudoku, and many other puzzles. It is often the most convenient (if not the most efficient technique for parsing, for the knapsack problem and other combinatorial optimization problems. I
Backtracking depends on user-given "black box procedures" that define the problem to be solved, the nature of the partial candidates, and how they are extended into complete candidates.
The pioneer string-processing language SNOBOL (1962) may have been the first to provide a built-in general backtracking facility.

Sudoku puzzle solved by backtracking.

Bellman–Ford runs in

O(|V|\cdot |E|)

time, where

|V|

and

|E|

are the number of vertices and edges respectively.

function BellmanFord(list vertices, list edges, vertex source)
   ::distance[],predecessor[]

   // This implementation takes in a graph, represented as
   // lists of vertices and edges, and fills two arrays
   // (distance and predecessor) with shortest-path
   // (less cost/distance/metric) information

   // Step 1: initialize graph
   for each vertex v in vertices:
       if v is source then distance[v] := 0
       else distance[v] := inf
       predecessor[v] := null

   // Step 2: relax edges repeatedly
   for i from 1 to size(vertices)-1:
       for each edge (u, v) with weight w in edges:
           if distance[u] + w < distance[v]:
               distance[v] := distance[u] + w
               predecessor[v] := u

   // Step 3: check for negative-weight cycles
   for each edge (u, v) with weight w in edges:
       if distance[u] + w < distance[v]:
           error "Graph contains a negative-weight cycle"
   return distance[], predecessor[]

In this example graph, assuming that A is the source and edges are processed in the worst order, from right to left, it requires the full |V|−1 or 4 iterations for the distance estimates to converge. Conversely, if the edges are processed in the best order, from left to right, the algorithm converges in a single iteration.


Class	Single-source shortest path problem (for weighted directed graphs)
Data structure	Graph
Worst case performance	$O (\|V\| \|E\|)$
Worst case space complexity	$O (\|V\|)$

BFS was invented in the late 1950s by E. F. Moore, who used to find the shortest path out of a maze, and discovered independently by C. Y. Lee as a wire routing algorithm

Breadth-first search
Order in which the nodes are expanded
Class	Search algorithm
Data structure	Graph
Worst case performance	$O(\|E\|) = O(b^d)$
Worst case space complexity	$O(\|V\|) = O(b^d)$

Depth-first

There are three types of depth-first traversal: pre-order, in-order, and post-order For a binary tree, they are defined as display operations recursively at each node, starting with the root node, whose algorithm is as follows:

Pre-order

Display the data part of root element (or current element)
Traverse the left subtree by recursively calling the pre-order function.
Traverse the right subtree by recursively calling the pre-order function.

In-order

Traverse the left subtree by recursively calling the in-order function.
Display the data part of root element (or current element).
Traverse the right subtree by recursively calling the in-order function.

Post-order

Traverse the left subtree by recursively calling the post-order function.
Traverse the right subtree by recursively calling the post-order function.
Display the data part of root element (or current element).

Depth-first search
Order in which the nodes are visited
Class	Search algorithm
Data structure	Graph
Worst case performance	$O(\|E\|)$ for explicit graphs traversed without repetition, $O(b^d)$ for implicit graphs with branching factor b searched to depth d
Worst case space complexity	$O(\|V\|)$ if entire graph is traversed without repetition, O(longest path length searched) for implicit graphs without elimination of duplicate nodes

Binary Search Tree

Pre-order: F, B, A, D, C, E, G, I, H

In-order: A, B, C, D, E, F, G, H, I

Post-order: A, C, E, D, B, H, I, G,F

Level-order: F, B, G, A, D, I, C, E, H

Offers

Pages

Sunday 25 December 2016

KNAPSACK PROBLEM

JUNE 2014 - PAPER III Q.No 62

CONVERSION OF INFIX EXPRESSION TO POSTFIX EXPRESSION

PROPERTIES OF BINARY TREES

JUNE 2007 - PAPER II Q.No 3

DECEMBER 2007 - PAPER II Q.No 23

JUNE 2009 - PAPER II Q.No. 27

DECEMBER 2009 - PAPER II Q.No 21

JUNE 2010 - PAPER II Q.No 23

DECEMBER 2011 - PAPER II Q.No. 50

Tuesday 6 October 2015

7.1 Bubble, Selection, Insertion Sorts

Bubble Sort

Analysis

Key terms

Constraints on bin sort

An example

7.5.1 Generalised Radix Sorting

Sample code

Analysis

Quick Sort - The Facts!

Can we do anything about this?

Median-of-3 Pivot

Random pivot

Why bother with quicksort then?

Thursday 12 February 2015

Depth-first

Pre-order

In-order

Post-order

Depth-first

Pre-order

In-order

Post-order